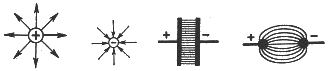Das
elektrische Feld
In der Umgebung eines elektrisch geladenen Körpers bzw.
zwischen zwei elektrisch geladenen Körpern besteht ein
elektrisches Feld. So bezeichnet man den Raum, in dem die Kräfte
der geladenen Körper wirken.
Ladung
Bei vielen Nichtleitern (Bernstein, Glas, Hartgummi u.a.) kann
durch Reibung die Oberfläche elektrisch geladen werden. Der
Oberfläche werden bei diesem Vorgang Elektronen entzogen oder
zugeführt:
Elektronenmangel: Körper ist positiv geladen
Elektronenüberschuß: Körper ist negativ geladen |
Zwischen elektrisch geladenen Körpern wirken Kräfte
| Gleichnahmig geladene Körper stoßen einander ab,
ungleichnahmig geladene Körper ziehen einander an. |
Aus diesem Grund sitzen die Ladungen leitender Körper stets
an der Oberfläche. Das Innere ist ladungs- und damit feldfrei.
Die Verteilung der Ladungen ist ungleich. An stärker gekrümmten
Stellen sitzen sie dichter. An Spitzen und Kanten können sie so
dicht sitzen, daß sie die Luft ionisieren und den Körper
verlassen (Spitzenwirkung).
Die gleichnahmig verteilten Elektronen eines ungeladenen Leiters
sammeln sich auf einer Körperhälfte unter der Wirkung der
Kräfte eines in die Nähe gebrachten geladenen Körpers (Influenz).
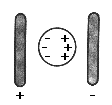 Demnach werden auch neutrale
Körper angezogen. Der Nachweis der Ladung kann nur durch
Abstoßung erfolgen.
Demnach werden auch neutrale
Körper angezogen. Der Nachweis der Ladung kann nur durch
Abstoßung erfolgen.
Nachweis und Messung der Ladung erfolgen mit Elektrometern. Auch
ruhende Ladungen werden (ebenso wie fließende) in Coulomb [C]
oder Ampéresekunden [As] angegeben.
Ein elektrisches Feld wird durch elektrische Kraftlinien
oder Feldlinien dargestellt.
| Die Feldlinien geben in jedem Punkt eines
elektrischen Feldes die Richtungen der dort wirkenden
Kraft an. |
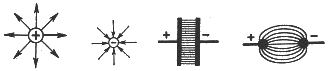
Eigenschaften: |
- Sie verlaufen von der positiven zur negativen
Ladung, haben also Anfang und Ende.
- Sie treten stets senkrecht aus der Oberfläche
eines leitenden Körpers aus.
- In Richtung der Feldlinien herrscht ein Zug, quer
zu ihnen ein Druck.
- Je nach Verlauf des Feldes nennt man das Feld radial,
homogen (bei parallelen
Feldlinien) oder inhomogen (bei
nichtparallelen Feldlinien).
|
Feldstärke
Die Stärke eines elektrischen Feldes wird durch die Kraft
ausgedrückt, die auf eine Punktladung in diesem Feld wirkt.
| Unter der Feldstärke versteht man das Verhältnis
der auf eine Ladung im Feld wirkenden Kraft zur Größe
dieser Ladung. |
.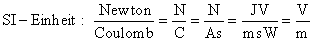
Entsprechend der Definition ist die elektrische Feldstärke
eine vektorielle Größe, d. h., sie ist durch
Betrag und Richtung bestimmt. Da es bei Berechnungen nur auf den
Betrag ankommt, wurde in der Schreibweise der folgenden
Gleichungen der vektorielle Charakter nicht berücksichtigt.
| Wenn |
E |
elektrische Feldstärke in V/m, |
| |
F |
Kraft, die im Feld auf eine Ladung Q wirkt, in N, |
| |
Q |
Ladung im Feld in C, |
Beachte:
In inhomogenen Feldern ist die Kraft örtlich verschieden, die
Gleichung liefert deshalb nur bei homogenen Feldern die für das
gesamte Feld geltende Feldstärke.
Die Bewegung einer Ladung im Feld entspricht einer Arbeit.
Folglich gilt:
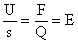
| Daraus folgt |
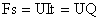 |
Somit ergibt sich für die elektrische Feldstärke ein
weiterer Ausdruck.
| Wenn |
E |
elektrische Feldstärke eines homogenen Feldes in
V/m, |
| |
d |
Abstand der beiden geladenen Platten, zwischen denen
das Feld existiert, in m, |
| |
U |
Spannung zwischen diesen Platten in V, |
Verschiebungsdichte
Die auf einen geladenen Körper (z.B. Platten eines
Kondensators) gebundenen Ladungen bestimmen die Größe der
herrschenden Feldstärke.
Unter der Verschiebungsdichte versteht man das Verhältnis der
Ladung zur Größe der geladenen Fläche.
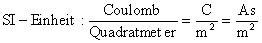
| Wenn |
D |
Verschiebungsdichte in C/m2, |
| |
Q |
Ladung, gebunden auf den Platten in C, |
| |
A |
Fläche der Platte in m2, |
Beachte:
Die Verschiebungsdichte entspricht der Ladungsdichte.
Verschiebungsdichte und Feldstärke müssen (als Ursache und
Wirkung) einander proportional sein.
| Wenn |
D |
Verschiebungsdichte in C/m2, |
| |
E |
elektrische Feldstärke in V/m, |
| |
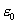 |
elektrische Feldkonstante = 8,85 * 10-12
As/Vm, |
Beachte:
Aus D=Q/A ergibt sich mit Q=DA die auf der gesamten Fläche
gebundene Ladungsmenge. Man bezeichnet sie mit Verschiebungsfluß
und gibt sie in Ampéresekunden (As) an.
Feldstärke an Leiteroberflächen
Mit Hilfe der Verschiebungsdichte läßt sich
die Feldstärke an der Oberfläche von Leitern bestimmen.
| Es gilt |
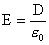 |
oder |
|
Feldstärke an der Kugeloberfläche
| Wenn |
E |
elektrische Feldstärke in V/m, |
| |
Q |
auf die Oberfläche gebundene Ladung
in C, |
| |
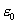 |
elektrische Feldkonstante = 8,85 * 10-12
As/Vm, |
| |
r |
Kugelradius in m, |
dann gilt für die Feldstärke an der
Kugeloberfläche
Beachte:
Die Konstante 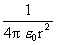 hat den Wert 8,99 * 109 Vm/C.
hat den Wert 8,99 * 109 Vm/C.
Über die Kapazität ergibt sich ein weiterer Ausdruck für die
Feldstärke auf der Kugeloberfläche.
| Wenn |
E |
elektrische Feldstärke in V/m, |
| |
U |
Spannung einer freistehenden Kugel
gegenüber Erde in V, |
| |
r |
Radius dieser Kugel in m, |
| dann gilt |
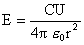 |
oder |
|
Beachte:
Bei einem geladenen Körper mit gekrümmter
Oberfläche ist die Feldstärke dem Krümmungsradius umgekehrt
proportional. Diese als Spitzenwirkung
(Spitzenentladung) bekannte Erscheinung führt zu Entladungen an
Stellen mit kleinem Krümmungsradius.

Quelle: Kuchling, Physik-Formeln und Gesetze, VEB Fachbuchverlag
Leipzig 1982.
Diese Seite wurde zuletzt am 10.08.2000
16:47:12 geändert.
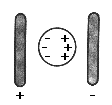 Demnach werden auch neutrale
Körper angezogen. Der Nachweis der Ladung kann nur durch
Abstoßung erfolgen.
Demnach werden auch neutrale
Körper angezogen. Der Nachweis der Ladung kann nur durch
Abstoßung erfolgen.